Érase una vez
mis experiencias con la estadística…
Soy una estudiante de enfermería que piensa que no solo hay que marcarse metas sino que debemos sobrepasarlas. Las estadísticas somos todos; ayuda a cambiarlas pero siempre A MEJOR.
La despedida
Hoy, 14 de Junio de 2013 el curso ha llegado a su fin.
Se ha pasado bastante rápido lo que indica que ha sido fluído e intenso. Muy intenso.
 Esta asignatura, a la que al principio no le daba mucha importancia, ha sido clave este cuatrimestre y siempre la he tenido presente pues, al igual que todas las ciencias empíricas (matemáticas e incluso la música) es algo que una vez aprendida nos acompaña el resto de nuestra vida de manera intensa y es la base de un buen conocimiento científico y la base para avanzar en nuestra carrera y en el mundo en general.
Esta asignatura, a la que al principio no le daba mucha importancia, ha sido clave este cuatrimestre y siempre la he tenido presente pues, al igual que todas las ciencias empíricas (matemáticas e incluso la música) es algo que una vez aprendida nos acompaña el resto de nuestra vida de manera intensa y es la base de un buen conocimiento científico y la base para avanzar en nuestra carrera y en el mundo en general.Ha sido un trabajo en equipo (profesor-alumnos) que ha ido mejorando con el paso de los días. La asignatura, a mi parecer tiene mucha dificultad pues partes de cero y en cuestión de nada tienes que tener conceptos importantísimos en tu mente que deberás recordar como tu propio nombre. Quitando las clases caóticas (pues toda asignatura empírica frecuenta dudas a cada minuto), han sido unas clases muy dinámicas donde hemos aprendido bastante.
Da pena decir adiós cuando interiorizamos una rutina pero ahora queda lo peor: el examen final, donde tendremos que plasmar y demostrar todo lo aprendido
Me despido con una sonrisa aunque me haya causado algún que otro disgusto la asignatura pero en general, me ha transmitido mucho conocimiento y madurez.
Ahora toca interiorizar y entender absolutamente todos los conceptos.
La suerte está echada y el curso terminado.
Gracias a mis compañeros y a mis profesores por amenizarme este camino tan intenso.
La estadística somos todos y todos nos ayudamos mutuamente para entenderla. Así todo irá siempre cuesta arriba. ¡Ánimo a todos! Si quieres, puedes.

Presentación de nuestro primer proyecto de investigación
El día de la presentación de nuestro primer proyecto de investigación lo recuerdo como algo...fatídico.
Mi grupo compuesto por Julia, Carlos, Sara y yo quisimos enfocar nuestro trabajo de la siguiente forma:
Quisimos comparar la alimentación que seguían los estudiantes universitarios en función del lugar de residencia: en sus hogares familiares o en pisos o residencias de estudiantes. Luego queríamos describir la percepción de cada uno de ellos.
 Ambos profesores, tanto Ponce como Sergio, nos dijeron que teníamos un buen marco teórico y un protocolo en general consistente. Sin embargo nuestro trabajo fue decayendo a medida que avanzábamos. Quizás influyó la falta de tiempo e incluso la poca comprensión sobre el tema 9 y 10, muy recientemente dados. Tuvimos que pedir varias tutorías con el profesor Sergio para que nos guíara y he de decir que sin su ayuda nuestro trabajo hubiera sido un fracaso. Tampoco fue un éxito pues los resultados estaban más (realizamos la T de Student y nos equivocamos en el grado de significación) y como dijo Ponce: "habíamos condenado al inocente".
Ambos profesores, tanto Ponce como Sergio, nos dijeron que teníamos un buen marco teórico y un protocolo en general consistente. Sin embargo nuestro trabajo fue decayendo a medida que avanzábamos. Quizás influyó la falta de tiempo e incluso la poca comprensión sobre el tema 9 y 10, muy recientemente dados. Tuvimos que pedir varias tutorías con el profesor Sergio para que nos guíara y he de decir que sin su ayuda nuestro trabajo hubiera sido un fracaso. Tampoco fue un éxito pues los resultados estaban más (realizamos la T de Student y nos equivocamos en el grado de significación) y como dijo Ponce: "habíamos condenado al inocente".Al final la evaluación de ambos profesores yo me veía en Agosto pasando cuestionarios pero finalmente llegaron las palabras más esperadas: "Aunque haya ido cuesta abajo, la teoría es bastante sólida. Estáis aprobados". Creo que ha sido el mayor alivio que he sentido en todo el curso (sin exagerar).
Tras la realización de este trabajo he podido comprobar que el campo de la investigación es un campo muy duro, el cuál requiere mucho tiempo y muchísimo esfuerzo y capacidad.
No estoy descontenta para ser el primer trabajo que hicimos contando con que el tiempo se nos echó encima.
A lo largo de esta asignatura hemos total el total apoyo de Sergio directamente y el seguimiento de Ponce indirectamente y hoy mismo, el último día de clase, he tenido una tutoría con Sergio para repasar errores del primer parcial. Me transmite seguridad y me ha aclarado bastantes conceptos.
Espero que el examen final esté más asentada y no cometas errores garrafales. Ya contamos con el factor experiencia tras la elaboración del trabajo de investigación y múltiples ejercicios resueltos en clase.


El segundo correspondía al tema 10.
1.- Predeterminar el tamaño de la
muestra necesaria para estudiar los niveles de glucosa plasmática de la
población de una zona básica de salud. Aceptamos un riesgo de error del 1% y
pretendemos una precisión de 5 mg. En una muestra reducida, la desviación
típica es de 15.
Daba como resultado: n=60
2.- A partir de ciertos estudios
se tiene la idea de que, operando inmediatamente a enfermos que ingresan en
estado de shock en un determinado servicio de un hospital, existe mayor
posibilidad de que el enfermo reaccione favorablemente. Para comprobar esta
hipótesis, se toman dos grupos de pacientes, a uno de los cuales se le opera
inmediatamente y al otro se espera a que se recupere del shock, obteniéndose
los siguientes resultados:
|
|
Recuperación
completa
|
Mejoría
|
Muerte
|
|
Operado
inmediatamente
|
10
|
7
|
3
|
|
Operado después de recuperación
|
5
|
3
|
2
|
A la vista del experimento ¿qué
se puede decir respecto a la hipótesis inicial? Identifica para ello la
hipótesis, las variables en estudio, el test adecuado y su resultado y
conclusión final.
El resultado fue: chi cuadrado=0.12 y grado de significación para nivel de confianza de 0.05 de 5.99.
Por lo tanto se acepta la hipótesis nula.
3.- Un investigador pretende
saber si las condiciones socioeconómicas influyen sobre la talla infantil. Para
ello, ha obtenido la talla de 20 niños de 5 años de edad, de dos condiciones
socioeconómicas contrastantes (alta y baja), que se exponen en la siguiente
tabla. Plantea la hipótesis pertinente, realiza la elección del test oportuno y
toma la decisión que proceda respecto a la hipótesis planteada.
|
Nivel
socioeconómico bajo
|
Nivel socioeconómico
alto
|
(x1- x‾1)
|
(x1- x‾1)2
|
(x2- x‾2)
|
(x2- x‾2)2
|
|
101
|
103
|
0.1
|
0.01
|
-2
|
4
|
|
102
|
105
|
11,1
|
1,21
|
0
|
0
|
|
100
|
104
|
-0,9
|
0,81
|
-1
|
1
|
|
104
|
106
|
3,1
|
9,61
|
1
|
1
|
|
102
|
108
|
1,1
|
1,21
|
3
|
9
|
|
99
|
100
|
-1,9
|
3,61
|
-5
|
25
|
|
102
|
108
|
1,1
|
1,21
|
3
|
9
|
|
103
|
104
|
2,1
|
4,41
|
-1
|
1
|
|
97
|
105
|
-3,9
|
15,21
|
0
|
0
|
|
99
|
107
|
-1,9
|
3,61
|
2
|
4
|
|
x‾1=100,9
|
x‾1=105
|
|
Σ (x1-
x‾1)2 = 40,9
|
|
Σ(x2 -
x‾2)2 = 54
|
Ejercicios del campus
Durante las últimas clases, para apoyar nuestro estudio de una forma práctica y que nos ayude a la hora de la evaluación final, Sergio colgó dos ejercicios en el campus de la universidad.
El primero correspondía al tema 9.
El primero correspondía al tema 9.
EJERCICIOS ESTADÍSTICA INFERENCIAL
1. Estamos interesados en conocer el consumo diario medio de cigarrillos entre los alumnos de Centros de Bachillerato de nuestra localidad. Seleccionada una muestra aleatoria de 100 alumnos se observó que fumaban una media de 8 cigarrillos diarios. Si admitimos que la varianza de dicho consumo es de 16 cigarrillos en el colectivo total, estime dicho consumo medio con un nivel de confianza del 95 %.
1. Estamos interesados en conocer el consumo diario medio de cigarrillos entre los alumnos de Centros de Bachillerato de nuestra localidad. Seleccionada una muestra aleatoria de 100 alumnos se observó que fumaban una media de 8 cigarrillos diarios. Si admitimos que la varianza de dicho consumo es de 16 cigarrillos en el colectivo total, estime dicho consumo medio con un nivel de confianza del 95 %.
Solución:
IC (95%) = (7.22, 8.78)
2. Se desea hacer una
estimación sobre la edad media de una determinada población. Calcula el tamaño
de la muestra necesario para poder realizar dicha estimación con un error menor
de medio año a un nivel de confianza del 99,73%. Se conoce de estudios previos
que la edad media de dicha población tiene una desviación típica igual a 3.
Solución:
De 324 personas, al menos, debe estar compuesta la muestra.
3. Tomada, al azar,
una muestra de 120 estudiantes de una Universidad, se encontró que 54 de ellos
hablaban inglés. Halle, con un nivel de confianza del 95%, un intervalo de
confianza para estimar la proporción de estudiantes que hablan el idioma inglés
entre los estudiantes de esa Universidad.
Solución:
IC (95%) = (0.54, 0.36)
Seminario 3
 En el último seminario comprobamos cuál era el alimento que produjo el brote de gastroenteritis entre los invitados de la fiesta parroquial americana. Lo hicimos gracias a la aplicación tal efetiva "Epi info" y a los conocimientos adquiridos en las clases anteriores. Calculamos el intervalo de confianza, la mediana, la moda, la desviación típica y la T de Student (al ser una variable cuantitativa (número de casos de gastroenteritis) y variable cualitativa (distintos alimentos consumidos)). Como teníamos la plantilla de los cuestionarios en Epi Info solo debíamos relacionar estas dos variables y Epi Info automáticamente nos calcula los resultados.
En el último seminario comprobamos cuál era el alimento que produjo el brote de gastroenteritis entre los invitados de la fiesta parroquial americana. Lo hicimos gracias a la aplicación tal efetiva "Epi info" y a los conocimientos adquiridos en las clases anteriores. Calculamos el intervalo de confianza, la mediana, la moda, la desviación típica y la T de Student (al ser una variable cuantitativa (número de casos de gastroenteritis) y variable cualitativa (distintos alimentos consumidos)). Como teníamos la plantilla de los cuestionarios en Epi Info solo debíamos relacionar estas dos variables y Epi Info automáticamente nos calcula los resultados. Cada miembro del seminario comparó un alimento diferente con el total de afectados y no afectados y observamos una gráfica que ya nos decía mucho de lo que podía ocurrir.
Cada miembro del seminario comparó un alimento diferente con el total de afectados y no afectados y observamos una gráfica que ya nos decía mucho de lo que podía ocurrir.Al final el alimento que yo elegí comparar (helado de vainilla) era el causante de la gastroenteritis pues daba una p menor a 0.05 y un valor de T significante.
Así finalizamos nuestras prácticas con esta aplicación y conocimos la incógnita del problama.
Sinceramente, estos tres seminarios me han parecido muy amenos e interesante y hemos aprendido mucho. Además añadir que Sergio, nuestro profesor, influye para que sean seminarios agradables y dinámicos, así como divertidos.
Tema 10. Hipótesis estadística. Test de hipótesis.
Bueno queridos amigos, compañeros, conocidos, desconocidos, investigadores todos, hemos llegado al final del curso, de este largo curso que me ha parecido un suspiro. Miro atrás y me veo el primer día de clase sin conocer a nadie preguntando si ésta era la clase de primero de enfermería. Y ahora hemos vivido millones de cosas juntos, buenas y malas, pero de todo hemos aprendido y en esta asignatura impartida desde el primer día del segundo cuatrimestre he aprendido bastante. Se nota la evolución de la asignatura. No es rectilínea. Tiene cuestas que subir. Cuestas que bajar. Parciales desastrosos. Ejercicios de clase infumables. Pero al fin y al cabo se trata de eso, de aprender. Nos ha ayudado además para afrontar nuestro proyecto de investigación, ese que me hizo temblar y del que más adelante os hablaré.

En este último tema vimos los contrastes de hipótesis, los cuales se utilizan para controlar los errores aleatorios. Una herramienta super útil para el proceso de inferencia estadística.
Con los intervalos de confianza del tema anterior nos hacemos una idea de un parámetro de una población dados un par de número entre los que confiamos que esté el valor desconocido.
Con los test o contrastes de hipótesis la estrategia cambia. Establece en principio una hipótesis acerca del valor del parámetro. Tras la recogida de datos analizamos la coherencia entre la hipótesis previamente establecida y los resultados obtenidos.
Con estos test podemos responder a preguntas de investigación porque permite cuantificar la contabilidad entre una hipótesis previa y los resultados.
Con esta herramienta siempre podemos contrastar la hipótesis nula (la que establece igualdad entre los grupos a comparar, es decir, la que no establece relación entre las variables de estudios.
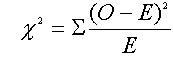 donde, O son los valores observados y E los
valores esperados.
donde, O son los valores observados y E los
valores esperados.
 , donde x1 es la media de la muestra 1 y la x2 la media de la muestra 2.
, donde x1 es la media de la muestra 1 y la x2 la media de la muestra 2.


En este último tema vimos los contrastes de hipótesis, los cuales se utilizan para controlar los errores aleatorios. Una herramienta super útil para el proceso de inferencia estadística.
Con los intervalos de confianza del tema anterior nos hacemos una idea de un parámetro de una población dados un par de número entre los que confiamos que esté el valor desconocido.
Con los test o contrastes de hipótesis la estrategia cambia. Establece en principio una hipótesis acerca del valor del parámetro. Tras la recogida de datos analizamos la coherencia entre la hipótesis previamente establecida y los resultados obtenidos.
Con estos test podemos responder a preguntas de investigación porque permite cuantificar la contabilidad entre una hipótesis previa y los resultados.
Con esta herramienta siempre podemos contrastar la hipótesis nula (la que establece igualdad entre los grupos a comparar, es decir, la que no establece relación entre las variables de estudios.
Controlar los errores aleatorios con los cálculos de
intervalos de confianza.
- Si la probabilidad es mayor de 0.5 aceptamos la hipótesis nula. Hipótesis alternativa mas plausible.
Test chi cuadrado: Compara dos variables cualitativas dicotómicas.
T de Student: Tenemos una variable continua y variable predictora dicotómica.
Errores de hipótesis:
El test de hipótesis mide la probabilidad de error que cometo si rechazo la hipótesis nula. Con una misma muestra podemos aceptar o rechazar la hipótesis nula. Todo depende del error alfa, que es la probabilidad de equivocarnos al rechazar la hipótesis nula (Ho).
El error alfa más pequeño con el que podemos rechazar la hipótesis nula se denomina error p. Lo más frecuente es rechazar la hipótesis nula con un grado de significación del 0.5.
A veces puede ocurrir que el test rechace la hipótesis nula y que la realidad diga lo contrario. A esto le denominamos errores alfa y pueden ser de tipo 1 (cuando la realidad acepta la Ho y el resultado del test la acepta) y error tipo 2 (la realidad rechaza la Ho y el test la acepta).
Estudiamos a fondo a continuación el test de chi cuadrado:
Se supone la hipótesis cierta y estudiamos cómo es de probable que siendo iguales dos grupos a comparar se obtengan resultados como los obtenidos o haber encontrado diferencias más grandes por grupos.
Ejercicio práctico:
Nos dan la siguiente tabla y tenemos que hallar las hipótesis y los resultados (si aceptamos o rechazamos la hipótesis nula planteada):
|
|
Positiva
|
Negativa
|
Total
|
|
Silvedema
|
11
|
15
|
26 (a)
|
|
Blastoestimulina
|
16
|
10
|
26 (b)
|
|
Total
|
27 (c)
|
25 (d)
|
52 (T)
|
Hipótesis nula: Silvedema y blastoestimulina no tienen
relación en cuanto a la efectividad.
Hipótesis alternativa 1: Silvedema es más efectiva que
blastoestimulina.
Hipótesis alternativa 2: Blastoestimulina es más efectiva
que silvedema.
Total de sujetos con silvedema (nS): 26
Total de sujetos con blastoestimulina (nB): 26
A continuación hacemos una tabla con frecuencias
esperadas (fe):
Fe1: a x
c/ T = 26 x 27/ 52= 13.5
Fe2: a x
d/T= 26 x 25/52 = 12.5
Fe3: b x
c/T = 26 x 27/52= 13.5
Fe4: b x
d/T= 26 x 26/52 = 12.5
Así:
|
|
Positiva
|
Negativa
|
Total
|
|
Silvedema
|
13.5
|
12.5
|
26
|
|
Blastoestimulina
|
13.5
|
12.5
|
26
|
|
Total
|
27
|
25
|
52
|
Aplicamos la formula de chi cuadrado:
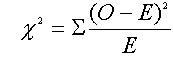 donde, O son los valores observados y E los
valores esperados.
donde, O son los valores observados y E los
valores esperados.
X² =(11-13.5)²/13.5 + (15-12.5)²/12.5 + (16-13.5)²/13.5 +
(10-12.5)²/12.5 = 1.92
Ahora calculamos el grado de libertad: (número de filas
-1)x(número de filas -1)=(2-1)x(2-1)=1.
Siempre que la tabla sea 2x2 el grado de libertad será
igual a 1.
Tomamos el nivel alfa p< 0.05 (probabilidad estándar
del 99%) y nos dirigimos a la tabla de chi cuadrado para obtener el valor de
significación teniendo en cuenta el grado de libertad y el nivel alfa.
Observamos que dicho valor es 3.84, por lo tanto para rechazar la hipótesis
nula, el valor de chi cuadrado deber ser mayor a 3.84. Como en este caso el
valor de chi cuadrado es de 1.92, aceptamos la hipótesis nula que dice que silvedema
y blastoestimulina no tienen relación en cuanto a la efectividad.
Ahora estudiamos a fondo el T de Student:
Ésta, como hemos dicho, se estudia cuando la variable independiente es cualitativa dicotómica y la variable dependiente es cuantitativa continua.
El grado de libertad se obtienen así: n1(columna 1)+(columna 2) -2
Para hallar la T realizamos la siguiente fórmula:
 , donde x1 es la media de la muestra 1 y la x2 la media de la muestra 2.
, donde x1 es la media de la muestra 1 y la x2 la media de la muestra 2.
La varianza común estimada (desviación típica al cuadrado) es:

Ejercicio resuelto:
Obtenemos dos grupos (cualitativos) con datos
cuantitativos. En el primer grupo la media es 8 y en el segundo es 12:
1 (grupo 1) 2
(grupo 2)
|
|
|
|
X1 X2
n1: 8 n2:12
Hipótesis nula: La variable independiente no tiene
relación con la variable dependiente.
El grado de libertad es: 8+12-2=18
Aplicamos la ecuación T de Student y el valor nos sale =
4.
El nivel alfa, al igual que en chi cuadrado es 0.05.
Nos vamos a la tabla de T de student teniendo en cuenta
el grado de libertad y el nivel alfa y observamos que para que exista
significación la T debe ser mayor a 1.73.
En este caso es mayor por lo que rechazaríamos la
hipótesis nula que hubiéramos previsto.
TEMA 9. ESTADISTICA INFERENCIAL: MUESTREO Y ESTIMACIÓN.
Podemos extraer resultados de la muestra a nivel
poblacional.
Para poder extrapolar los datos tiene que tener validez
interna, que garantiza que se puedan extrapolar a la población de referencia.
Al conjunto de pacientes llamamos poblaciones y al conjunto de individuos
concretos se le llama muestra. A la cantidad: tamaño muestral.
Al conjunto de procedimientos que permiten elegir
muestras de tal forma que estas reflejen las características de la población le
llamamos técnicas de muestreo.
Siempre que trabajamos con muestras asumimos cierto error
(error aleatorio). El muestreo probabilístico lo veremos mas adelante.
El error asociado a pesar de que sea una muestra
representativa, siempre podemos cometer un error aleatorio. Tenemos muchos
errores si usamos muestreo por
voluntarios.
Ejemplo inferencia
Tiempo de curación de ulceras en una muestra de 100
pacientes. El grupo de primera fila en su área a cogido una muestra de personas
con ulcera (100) ha ido calculando cuanto tiempo tarda en curarse la ulcera y a
sacado una media: 53.77 días.
La segunda fila es otro grupo del mismo población y le da
otra media: 57.08.
Y así sucesivamente.
Si en la clase todos
los grupos estudiamos lo mismo y tenemos un histograma con diferencias
medias de distintas muestras de una misma población.
Si en Sevilla hay 200 mil personas con ulceras, podemos
sacar muchas muestras representativas de ahí. Existe variabilidad biológica y
puede pasar que haya un grupo que cure a 62 y otro a 65.
La media total son 57.77. en total todos estos estudios
se los han hecho a 20 mil pacientes.
Concepto nuevo:
ERROR ESTANDAR
E s una medida que estima y que pretende captar la
variabilidad: rango que se mueven en torno a una media concreta.
Calcula (similar a la desviación típica: valor real que
abre el rango entre la media y un 68% de la población. Sabemos que el 68% se
engloba en el +/-). El error es una estimación de cómo puede variar en torno a
la media.
El valor real no lo conocemos porque es una muestra.
Conocemos el valor de la muestra. El error estándar nos permite presumir como
un intervalo en el cual se mueve el intervalo de la media.
Si el error estándar estima el valor real que va a tener
la curación de la ulcera, mientras más pequeño es el error , más cerca esta del
valor real.
Mientras mayor sea la muestra, el error estándar es
menor: error aleatorio (se materializa en
el erro estándar)
El estándar dice que a mayor muestra menor error
estándar, mayor precisión.
La media real de la población si estimamos que es la
misma de la muestra, error poblacional medio es el estándar. Mientras mas
pequeño sea el error mas cerca del valor real estaré. Mientras mas muestra
tenga mas me acerco a la población general.
El erro estándar se calcula: desviación típica entre raíz
cuadrada de n (tamaño de mi muestra).
Si el intervalo de confianza del 95% cometemos un error
del 5%. La probabilidad que manejo x 1-probablidad que manejo.
Si yo quiero tener un intervalo o confianza del 95%, la probabilidad
de acertar es de 0.95 en tasa. La probabilidad que yo manejo x 1-0.5 entre la
muestra y todo a la raíz cuadrada.
Teorema central
del límite
Lo ideal y normal es exista una distribución de valores
que siguen una distribución normal.
Englobar en unos términos y que vaya de manera aislada
hacia los extremos.
Pero esto no es siempre así: los datos no se distribuyen
de manera normal. Existe un teorema que dice que si se cogen varias muestras y
se le aplica la media, las medias de las medias de las muestras se van a
agrupar de manera normal. Porque va cogiendo valores aislados y cada vez lo va
centrando mas y cada vez se va concentrando en la cota media. A mas población y
cada vez mas medias, la desviación típica y el erro estándar cada vez se hará
mas pequeño. Cada vez tendera mas al centro. La distribución sigue una
distribución normal con un error estándar que cada vez se acerca mas a la
desviación típica.
El peso no sigue una distribución normal porque la media
esta sobre 80 de la población adulta y la mayor concentración está antes de la
media asi que no es una distribución normal sino con curva a la derecha.
Vamos cogiendo una persona de manera aleatoria de la
población y construyo las medias de los datos que nos va dando.
Representamos un histograma con los valores de los individuos.
Mientras mas muestra, mas se parece la grafica de la muestra a la grafica de la
población.
Primera muestra aleatoria tomamos un valor extremo asi
que la media se sitúa mas al centro: estimación de la media. Las medias
muestrales se acerca cada vez mas al centro con muestra de tamaño 2. Raya
horizontal: desviación. Esto es la media de dos individuos cada vez.
Después se escogen 10 individuos y hacen la media y este
es un valor que da una media diferente a la media de la población. Aumentamos a
10 el tamaño de la muestra. Se parece mucho a la distribución normal. Esto
afirma el teorema del límite central. La media total de la distribución es
igual que la media de la población.
+/- 1Sà
68, 26 % de las observaciones (muestras)
+/- 2Sà
95-45 % de las observaciones
+/- 1.66S à95%
de las observaciones
+/- 3Sà
99.73% de las observaciones
+/- 2.58 Sà
99% de las observaciones
El valor z se obtiene multiplicándolo a la desviación (S)
Se estima como numero entero 95 y 0.05 pero hay multitud
de valores.
Cuando diseñamos el estudio estimamos el nivel de
confianza (95,99%). Si creemos que hay relación muy importante entre dos
variables, nos situamos en un 99%. Si tenemos un valor menor del 1%, hablamos
de relación contra-efecto sí o sí.
INTERVALO DE
CONFIANZA
Son estimadores de población que contempla un rango donde
en el 95% de probabilidad va a estar el valor real.
Esto se puede calcular a cualquier estimador: OR, Riesgo
relativo…
De un parámetro: estimador +- z y valor estándar.
El error estándar x z es el valor superior y el valor
inferior. El máximo sería la suma.
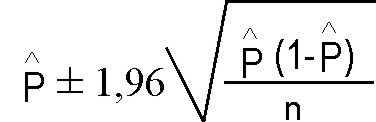
(*) 1, 96 es el valor z, que como vimos antes puede adoptar otros valores en función del nivel de confianza.
Esta fórmula es para proporciones y la "p" es el estimador.
Para medias se utiliza la siguiente fórmula:
IC= estimador +/- z x ES
Procedimiento muestral: técnica de muestreo
Un muestreo es un método tal que al escoger un grupo pequeño de una población podemos tener un grado de probabilidad de que ese pequeño grupo posea las características de la población que estamos estudiando.
La población general de la que queremos obtener conclusiones la vamos a elegir al azar, para obtener la muestra y a partir de ésta hacer inferencia de la población entera.
Tipos de muestreo:
Probabilistico: Todos los sujetos de la población tienen una probabilidad distinta de cero en la seleccion de la muestra. Es el método que consiste en extraer una parte de una población o universo, de tal forma que todas las muestras posibles de tamaño fijo tengan la misma posibilidad de ser seleccionados.
Simple: Se caracteriza porque cada unidad tiene la porbabilidad equitativa de ser incluida en la muestra.
Sistemático: Similar al aleatorio simple, donde cada unidad del universo tiene la misma probabilidad de ser seleccionado.
Sea 5 el intervalo para la selección de cada unidad muestra: Cada 5 personas se selecciona: 5, 10, 15... y así sucesivamente hasta llegar a 100.
Estratificado: Se caracteriza por la subdivisión de la pobalción en subgrupos o estratos, debido a que las variables principales que deben someterse a estudio presentan cierta variabilidad o distribución conocida que puede afectar a los resultados.
Conglomerado: Se usa cuando no se dispone de una lista detallada y enumerada de cada una de las unidades que conforman el universo y resulta muy complejo elaborarla. Las inferencias que se hacen en una muestra conglomerada no son confiables como las que se obtienen en un estudio hecho por muestreo aleatorio.
Muestra no probabilística: Me interesa un grupo concreto. Personas que están expuestas
a algo concreto, si nos vamos intencionadamente a esas personas excluimos a las
que nunca han estado expuesta al factor.
Por cuotas: quiero
tener mitad de hombre y mujer, esto es una cuota: 50% y 50%. Las poblaciones no
siempre son 50 y 50. El ejemplo de los sesgos: sesgo de selección porque no hay el
mismo numero de hombres (esto no es un sesgo) sino que intencionadamente se ha
escogido así.
Accidental: paciente
con tensión, se apunta. Cogemos a pacientes que por casualidad ese dia
acudieron al centro de salud (no todas tienen la misma probablidad de
participar en el estudio, sino solo aquellas que ese dia fueron al centro de
salud)
Tamaño de la muestra
Va a depender de la varianza (variabilidad de la población),
tamaño de la población y de la confianza que nosotros tenemos.
El tamaño se multiplica por la varianza poblacional y se
divide por el error estándar o presicion al cuadrado.
Si tras esta operación se cumple el resultado N> n(n-1), el calculo del tamaño muestral terminal aquí.
Y a la clase siguiente...


·
Distribución
normal y forma de distribución: asimetría y curtosis.
Distribución de Gauss o distribución gaussiana: sirve para
variables continuas. Un ejemplo de variable continua es el peso, la tensión
arterial, la talla… Y la distribución es la que sirve como referencia de la
distribución normal: la gráfica tiene forma acampanada: la campana de gauss.

Propiedades:
En el punto medio se concentra las medidas de tendencia:
media mediana y moda.
Características: el punto medio corta la campana de
manera simétrica. Ahí está la mediana.
Los bordecitos extremos hacen función de asíntota: se
aproxima hasta el infinito y nunca llega a tocarla.
Tiene muy poca representación: el 1%.
Si tomamos el 90% tenemos la totalidad de la confianza
del estudio puesto que es muy poco probable y sería un estudio muy fiable.
Parámetros
estadísticos o parámetros:
Los parámetros hacen referencia a la población. Todo esto
es a nivel ideal o pablacional.
La media contempla el 68% de la población en la gráfica
de distribuciones normales.
Una vez la desviación típica contempla eso.
El punto donde queda la desviación típico es el punto de
inflexión: la campana cambia la curva de cóncava a convexa. Se encuentra justo
en la +/- desviación típico.
3 veces la desviación típica ya contempla el 99%.
Dada una media y una desviación típica si tenemos que
calcular los valores en los que se engolaba el 95% de la muestra: variación
típica x el valor y sumárselo o restárselo a la media.
No siempre la media y la mediana coincide en el mismo
punto.
Moda>media la curva tira hacia la izquierda.
Coeficiente de
asimetría de una variable: Como se distribuye los datos en torno a su media.
Formula que contempla el grado de asimetría y da un
valor.
Si el valor es = 0, la curva es símetrica
Si el grado es +, curva a la izq.
Si es -, curva a la izquierda.
De La otra formula depende el apuntamiento normal, abombado
hacia arriba y hacia abajo.
Resultado:
G2: grado de
curtosis o apuntamiento.
G2=0, la distribución es normal (mesocúrtica de
curtosis). En torno al eje de simetría .
G2=+ , distribución hacia arriba (leptocúrtica)
G2=-, distribución mas o menos plana (platicurtica).
Mientras mas dispersa de la media, mas ancha es la campana. Mientras mas unida
al eje de simetría, mas leptocurtica será la campana.

Suscribirse a:
Comentarios (Atom)



