En este último tema vimos los contrastes de hipótesis, los cuales se utilizan para controlar los errores aleatorios. Una herramienta super útil para el proceso de inferencia estadística.
Con los intervalos de confianza del tema anterior nos hacemos una idea de un parámetro de una población dados un par de número entre los que confiamos que esté el valor desconocido.
Con los test o contrastes de hipótesis la estrategia cambia. Establece en principio una hipótesis acerca del valor del parámetro. Tras la recogida de datos analizamos la coherencia entre la hipótesis previamente establecida y los resultados obtenidos.
Con estos test podemos responder a preguntas de investigación porque permite cuantificar la contabilidad entre una hipótesis previa y los resultados.
Con esta herramienta siempre podemos contrastar la hipótesis nula (la que establece igualdad entre los grupos a comparar, es decir, la que no establece relación entre las variables de estudios.
Controlar los errores aleatorios con los cálculos de
intervalos de confianza.
- Si la probabilidad es mayor de 0.5 aceptamos la hipótesis nula. Hipótesis alternativa mas plausible.
Test chi cuadrado: Compara dos variables cualitativas dicotómicas.
T de Student: Tenemos una variable continua y variable predictora dicotómica.
Errores de hipótesis:
El test de hipótesis mide la probabilidad de error que cometo si rechazo la hipótesis nula. Con una misma muestra podemos aceptar o rechazar la hipótesis nula. Todo depende del error alfa, que es la probabilidad de equivocarnos al rechazar la hipótesis nula (Ho).
El error alfa más pequeño con el que podemos rechazar la hipótesis nula se denomina error p. Lo más frecuente es rechazar la hipótesis nula con un grado de significación del 0.5.
A veces puede ocurrir que el test rechace la hipótesis nula y que la realidad diga lo contrario. A esto le denominamos errores alfa y pueden ser de tipo 1 (cuando la realidad acepta la Ho y el resultado del test la acepta) y error tipo 2 (la realidad rechaza la Ho y el test la acepta).
Estudiamos a fondo a continuación el test de chi cuadrado:
Se supone la hipótesis cierta y estudiamos cómo es de probable que siendo iguales dos grupos a comparar se obtengan resultados como los obtenidos o haber encontrado diferencias más grandes por grupos.
Ejercicio práctico:
Nos dan la siguiente tabla y tenemos que hallar las hipótesis y los resultados (si aceptamos o rechazamos la hipótesis nula planteada):
|
|
Positiva
|
Negativa
|
Total
|
|
Silvedema
|
11
|
15
|
26 (a)
|
|
Blastoestimulina
|
16
|
10
|
26 (b)
|
|
Total
|
27 (c)
|
25 (d)
|
52 (T)
|
Hipótesis nula: Silvedema y blastoestimulina no tienen
relación en cuanto a la efectividad.
Hipótesis alternativa 1: Silvedema es más efectiva que
blastoestimulina.
Hipótesis alternativa 2: Blastoestimulina es más efectiva
que silvedema.
Total de sujetos con silvedema (nS): 26
Total de sujetos con blastoestimulina (nB): 26
A continuación hacemos una tabla con frecuencias
esperadas (fe):
Fe1: a x
c/ T = 26 x 27/ 52= 13.5
Fe2: a x
d/T= 26 x 25/52 = 12.5
Fe3: b x
c/T = 26 x 27/52= 13.5
Fe4: b x
d/T= 26 x 26/52 = 12.5
Así:
|
|
Positiva
|
Negativa
|
Total
|
|
Silvedema
|
13.5
|
12.5
|
26
|
|
Blastoestimulina
|
13.5
|
12.5
|
26
|
|
Total
|
27
|
25
|
52
|
Aplicamos la formula de chi cuadrado:
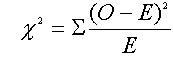donde, O son los valores observados y E los
valores esperados.
X² =(11-13.5)²/13.5 + (15-12.5)²/12.5 + (16-13.5)²/13.5 +
(10-12.5)²/12.5 = 1.92
Ahora calculamos el grado de libertad: (número de filas
-1)x(número de filas -1)=(2-1)x(2-1)=1.
Siempre que la tabla sea 2x2 el grado de libertad será
igual a 1.
Tomamos el nivel alfa p< 0.05 (probabilidad estándar
del 99%) y nos dirigimos a la tabla de chi cuadrado para obtener el valor de
significación teniendo en cuenta el grado de libertad y el nivel alfa.
Observamos que dicho valor es 3.84, por lo tanto para rechazar la hipótesis
nula, el valor de chi cuadrado deber ser mayor a 3.84. Como en este caso el
valor de chi cuadrado es de 1.92, aceptamos la hipótesis nula que dice que silvedema
y blastoestimulina no tienen relación en cuanto a la efectividad.
Ahora estudiamos a fondo el T de Student:
Ésta, como hemos dicho, se estudia cuando la variable independiente es cualitativa dicotómica y la variable dependiente es cuantitativa continua.
El grado de libertad se obtienen así: n1(columna 1)+(columna 2) -2
Para hallar la T realizamos la siguiente fórmula:
, donde x1 es la media de la muestra 1 y la x2 la media de la muestra 2.
La varianza común estimada (desviación típica al cuadrado) es:
Ejercicio resuelto:
Obtenemos dos grupos (cualitativos) con datos
cuantitativos. En el primer grupo la media es 8 y en el segundo es 12:
1 (grupo 1) 2
(grupo 2)
|
|
|
|
X1 X2
n1: 8 n2:12
Hipótesis nula: La variable independiente no tiene
relación con la variable dependiente.
El grado de libertad es: 8+12-2=18
Aplicamos la ecuación T de Student y el valor nos sale =
4.
El nivel alfa, al igual que en chi cuadrado es 0.05.
Nos vamos a la tabla de T de student teniendo en cuenta
el grado de libertad y el nivel alfa y observamos que para que exista
significación la T debe ser mayor a 1.73.
En este caso es mayor por lo que rechazaríamos la
hipótesis nula que hubiéramos previsto.
No hay comentarios:
Publicar un comentario