EL BLOG DE ANAPÍ. ESTADÍSTICA Y TIC: TEMA 9. ESTADISTICA INFERENCIAL: MUESTREO Y ESTIMACIÓN.

Podemos extraer resultados de la muestra a nivel poblacional.

Para poder extrapolar los datos tiene que tener validez interna, que garantiza que se puedan extrapolar a la población de referencia. Al conjunto de pacientes llamamos poblaciones y al conjunto de individuos concretos se le llama muestra. A la cantidad: tamaño muestral.

Al conjunto de procedimientos que permiten elegir muestras de tal forma que estas reflejen las características de la población le llamamos técnicas de muestreo.

Siempre que trabajamos con muestras asumimos cierto error (error aleatorio). El muestreo probabilístico lo veremos mas adelante.

El error asociado a pesar de que sea una muestra representativa, siempre podemos cometer un error aleatorio. Tenemos muchos errores si usamos muestreo por voluntarios.

Ejemplo inferencia

Tiempo de curación de ulceras en una muestra de 100 pacientes. El grupo de primera fila en su área a cogido una muestra de personas con ulcera (100) ha ido calculando cuanto tiempo tarda en curarse la ulcera y a sacado una media: 53.77 días.

La segunda fila es otro grupo del mismo población y le da otra media: 57.08.

Y así sucesivamente.

Si en la clase todos los grupos estudiamos lo mismo y tenemos un histograma con diferencias medias de distintas muestras de una misma población.

Si en Sevilla hay 200 mil personas con ulceras, podemos sacar muchas muestras representativas de ahí. Existe variabilidad biológica y puede pasar que haya un grupo que cure a 62 y otro a 65.

La media total son 57.77. en total todos estos estudios se los han hecho a 20 mil pacientes.

Concepto nuevo: ERROR ESTANDAR

E s una medida que estima y que pretende captar la variabilidad: rango que se mueven en torno a una media concreta.

Calcula (similar a la desviación típica: valor real que abre el rango entre la media y un 68% de la población. Sabemos que el 68% se engloba en el +/-). El error es una estimación de cómo puede variar en torno a la media.

El valor real no lo conocemos porque es una muestra. Conocemos el valor de la muestra. El error estándar nos permite presumir como un intervalo en el cual se mueve el intervalo de la media.

Si el error estándar estima el valor real que va a tener la curación de la ulcera, mientras más pequeño es el error , más cerca esta del valor real.

Mientras mayor sea la muestra, el error estándar es menor: error aleatorio (se materializa en el erro estándar)

El estándar dice que a mayor muestra menor error estándar, mayor precisión.

La media real de la población si estimamos que es la misma de la muestra, error poblacional medio es el estándar. Mientras mas pequeño sea el error mas cerca del valor real estaré. Mientras mas muestra tenga mas me acerco a la población general.

El erro estándar se calcula: desviación típica entre raíz cuadrada de n (tamaño de mi muestra).

Si el intervalo de confianza del 95% cometemos un error del 5%. La probabilidad que manejo x 1-probablidad que manejo.

Si yo quiero tener un intervalo o confianza del 95%, la probabilidad de acertar es de 0.95 en tasa. La probabilidad que yo manejo x 1-0.5 entre la muestra y todo a la raíz cuadrada.

Teorema central del límite

Lo ideal y normal es exista una distribución de valores que siguen una distribución normal.

Englobar en unos términos y que vaya de manera aislada hacia los extremos.

Pero esto no es siempre así: los datos no se distribuyen de manera normal. Existe un teorema que dice que si se cogen varias muestras y se le aplica la media, las medias de las medias de las muestras se van a agrupar de manera normal. Porque va cogiendo valores aislados y cada vez lo va centrando mas y cada vez se va concentrando en la cota media. A mas población y cada vez mas medias, la desviación típica y el erro estándar cada vez se hará mas pequeño. Cada vez tendera mas al centro. La distribución sigue una distribución normal con un error estándar que cada vez se acerca mas a la desviación típica.

El peso no sigue una distribución normal porque la media esta sobre 80 de la población adulta y la mayor concentración está antes de la media asi que no es una distribución normal sino con curva a la derecha.

Vamos cogiendo una persona de manera aleatoria de la población y construyo las medias de los datos que nos va dando.

Representamos un histograma con los valores de los individuos. Mientras mas muestra, mas se parece la grafica de la muestra a la grafica de la población.

Primera muestra aleatoria tomamos un valor extremo asi que la media se sitúa mas al centro: estimación de la media. Las medias muestrales se acerca cada vez mas al centro con muestra de tamaño 2. Raya horizontal: desviación. Esto es la media de dos individuos cada vez.

Después se escogen 10 individuos y hacen la media y este es un valor que da una media diferente a la media de la población. Aumentamos a 10 el tamaño de la muestra. Se parece mucho a la distribución normal. Esto afirma el teorema del límite central. La media total de la distribución es igual que la media de la población.

+/- 1Sà 68, 26 % de las observaciones (muestras)

+/- 2Sà 95-45 % de las observaciones

+/- 1.66S à95% de las observaciones

+/- 3Sà 99.73% de las observaciones

+/- 2.58 Sà 99% de las observaciones

El valor z se obtiene multiplicándolo a la desviación (S)

Se estima como numero entero 95 y 0.05 pero hay multitud de valores.

Cuando diseñamos el estudio estimamos el nivel de confianza (95,99%). Si creemos que hay relación muy importante entre dos variables, nos situamos en un 99%. Si tenemos un valor menor del 1%, hablamos de relación contra-efecto sí o sí.

INTERVALO DE CONFIANZA

Son estimadores de población que contempla un rango donde en el 95% de probabilidad va a estar el valor real.

Esto se puede calcular a cualquier estimador: OR, Riesgo relativo…

De un parámetro: estimador +- z y valor estándar.

El error estándar x z es el valor superior y el valor inferior. El máximo sería la suma.

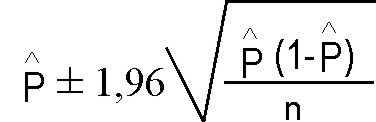
(*) 1, 96 es el valor z, que como vimos antes puede adoptar otros valores en función del nivel de confianza.

Esta fórmula es para proporciones y la "p" es el estimador.

Para medias se utiliza la siguiente fórmula:

IC= estimador +/- z x ES

Procedimiento muestral: técnica de muestreo

Un muestreo es un método tal que al escoger un grupo pequeño de una población podemos tener un grado de probabilidad de que ese pequeño grupo posea las características de la población que estamos estudiando.

La población general de la que queremos obtener conclusiones la vamos a elegir al azar, para obtener la muestra y a partir de ésta hacer inferencia de la población entera.

Tipos de muestreo:

Probabilistico: Todos los sujetos de la población tienen una probabilidad distinta de cero en la seleccion de la muestra. Es el método que consiste en extraer una parte de una población o universo, de tal forma que todas las muestras posibles de tamaño fijo tengan la misma posibilidad de ser seleccionados.

Simple: Se caracteriza porque cada unidad tiene la porbabilidad equitativa de ser incluida en la muestra.

Sistemático: Similar al aleatorio simple, donde cada unidad del universo tiene la misma probabilidad de ser seleccionado.

Sea 5 el intervalo para la selección de cada unidad muestra: Cada 5 personas se selecciona: 5, 10, 15... y así sucesivamente hasta llegar a 100.

Estratificado: Se caracteriza por la subdivisión de la pobalción en subgrupos o estratos, debido a que las variables principales que deben someterse a estudio presentan cierta variabilidad o distribución conocida que puede afectar a los resultados.

Conglomerado: Se usa cuando no se dispone de una lista detallada y enumerada de cada una de las unidades que conforman el universo y resulta muy complejo elaborarla. Las inferencias que se hacen en una muestra conglomerada no son confiables como las que se obtienen en un estudio hecho por muestreo aleatorio.

Muestra no probabilística: Me interesa un grupo concreto. Personas que están expuestas a algo concreto, si nos vamos intencionadamente a esas personas excluimos a las que nunca han estado expuesta al factor.

Por cuotas: quiero tener mitad de hombre y mujer, esto es una cuota: 50% y 50%. Las poblaciones no siempre son 50 y 50. El ejemplo de los sesgos: sesgo de selección porque no hay el mismo numero de hombres (esto no es un sesgo) sino que intencionadamente se ha escogido así.

Accidental: paciente con tensión, se apunta. Cogemos a pacientes que por casualidad ese dia acudieron al centro de salud (no todas tienen la misma probablidad de participar en el estudio, sino solo aquellas que ese dia fueron al centro de salud)

Tamaño de la muestra

Va a depender de la varianza (variabilidad de la población), tamaño de la población y de la confianza que nosotros tenemos.

El tamaño se multiplica por la varianza poblacional y se divide por el error estándar o presicion al cuadrado.